to prove i equals infinity/zero

let
u=5,v=4,w= -1,x=zero,y=infinity,z=1 and i = square root of (-1)

firstly take

- 20 = - 20
which can be written as
=> 16-36 = 25-45
by adding (81/4) on both sides we get
=> 16-36+(81/4) = 25-45+(81/4)
by writing the above eqn like this
=> ((4)2 -(2*4*(9/2)) +(9/2)2) = ((5)2 -(2*5*(9/2)) +(9/2)2)
which is of the form
=> (a-b)2 = a2 + b2 -2ab
here
=> a = 4 a = 5
b = 9/2 b = 9/2
from this we can write the above equation as
=> (4-(9/2)) 2 = (5-(9/2))2
by taking square root on both sides we get
=> +- (4-(9/2)) = +- (5-(9/2))
according to axioms when both sides are equal and having the same signs on both sides then both sides are positively equated to each other
=> 4 - (9/2) = 5 - (9/2)
by shifting -(9/2) from left side to right side we get
=> 4 = 5 - (9/2) +(9/2)
then as 9/2 gets cancelled we get
=> 4 = 5
then substituting corresponding variables for result we get
=> v = u ........................................eqn1
then by shifting v we get
=> 0 = u-v
here by entering values of u and v we prove that 0=1
i.e 0 = 5-4 => 0 = 1 ..............................eqn2
again here by substituting the corresponding variables to result we get
=> x = z
here by cross multiplying x to z quadrant we get
=> 1 = (z/x)
then again by substituting corresponding values of z and x we get
=> 1 = (1/0)
as we know that (1/0) is infinity
=> 1 = infinity ................................eqn3
again by representing result with corresponding variables we get
=> z = y
then by mathematical laws
if a=b and b=c then a=c we get
=>x = y
here by substituting there values we get
=> zero = infinity
from eqn 1 by moving u to the other side we get
=> v-u = 0
which is equal to
=> 4-5 = 0 => -1 = 0 ....................eqn 4
again by using laws here we can write
-1 = 0 and 0 = infinity therfore
-1 = infinity ..........................eqn 5
again in eqn 4
=> -1 = 0 by taking square root on both sides we get
=> i = 0 .............................eqn6
therefore i = 0
similarly
by eqn 5
=> -1 = 0 and by taking square root of both sides we get
=> i = root of infinity (which is undefined)
again back with eqn 6 i.e
=> i = 0
by mathematical laws we can write it as
=> i = infinity (because i = 0 and 0 = infinity so i = infinity)




Extra tips--->
1)by using eqn 2 any number can be proved to zero (i.e by multiplying both sides by any number)
2)by using eqn 3 any number can be proved to infinity (i.e by multiplying both sides by any number)
3)by using eqns above u can prove which ever number present to which ever number u wan't


isn't this amazing

To prove zero equals infinity

let
u=5,v=4,x=zero,y=infinity,z=1

firstly take

- 20 = - 20
which can be written as
=> 16-36 = 25-45
by adding (81/4) on both sides we get
=> 16-36+(81/4) = 25-45+(81/4)
by writing the above eqn like this
=> ((4)2 -(2*4*(9/2)) +(9/2)2) = ((5)2 -(2*5*(9/2)) +(9/2)2)
which is of the form
=> (a-b)2 = a2 + b2 -2ab
here
=> a = 4 a = 5
b = 9/2 b = 9/2
from this we can write the above equation as
=> (4-(9/2)) 2 = (5-(9/2))2
by taking square root on both sides we get
=> +- (4-(9/2)) = +- (5-(9/2))
according to axioms when both sides are equal and having the same signs on both sides then both sides are positively equated to each other
=> 4 - (9/2) = 5 - (9/2)
by shifting -(9/2) from left side to right side we get
=> 4 = 5 - (9/2) +(9/2)
then as 9/2 gets cancelled we get
=> 4 = 5
then substituting corresponding variables for result we get
=> v = u
then by shifting v we get
=> 0 = u-v ........................................eqn1
here by entering values of u and v we prove that 0=1
i.e 0 = 5-4 => 0 = 1 ..............................eqn2
again here by substituting the corresponding variables to result we get
=> x = z
here by cross multiplying x to z quadrant we get
=> 1 = (z/x)
then again by substituting corresponding values of z and x we get
=> 1 = (1/0)
as we know that (1/0) is infinity
=> 1 = infinity ................................eqn3
again by representing result with corresponding variables we get
=> z = y
then by mathematical laws
if a=b and b=c then a=c we get
=>x = y
here by substituting there values we get
=> zero = infinity
hence proved.

Extra tips--->
1)by using eqn 2 any number can be proved to zero (i.e by multiplying both sides by any number)
2)by using eqn 3 any number can be proved to infinity (i.e by multiplying both sides by any number)



isn't this amazing

To prove 4 = 5

let

- 20 = - 20
which can be written as
=> 16-36 = 25-45
by adding (81/4) on both sides we get
=> 16-36+(81/4) = 25-45+(81/4)
by writing the above eqn like this
=> ((4)2 -(2*4*(9/2)) +(9/2)2) = ((5)2 -(2*5*(9/2)) +(9/2)2)
which is of the form
=> (a-b)2 = a2 + b2 -2ab
here
=> a = 4 a = 5
b = 9/2 b = 9/2
from this we can write the above equation as
=> (4-(9/2)) 2 = (5-(9/2))2
by taking square root on both sides we get
=> +- (4-(9/2)) = +- (5-(9/2))
according to axioms when both sides are equal and having the same signs on both sides then both sides are positively equated to each other
=> 4 - (9/2) = 5 - (9/2)
by shifting -(9/2) from left side to right side we get
=> 4 = 5 - (9/2) +(9/2)
then as 9/2 gets cancelled we get
=> 4 = 5



isn't this amazing

tips to prove any number to any number directly

• Select the numbers which are to be proved equal to each other ex: 2 and 7
• Then write down the selected number multiples with negative sign
  

i.e -14 = -14

• Then write the numbers on both lhs and rhs in the form of square of selected number substracted by some number so that their results produce the numbers which are written above them i.e 4-18 = 49-63
• Then add square of a number on both sides which must be derived from dividing the substracting number by selected number and again by 2 i.e (-18)/(2)=-9 again divided by 2 gives -9/2 and similarly -63/7 = -9 again divided by 2 gives -9/2 note that the number obtained on both sides will be the same number.Then square the number and add it to both sides i.e 4-18+(81/4) = 49-63+(81/4)
• Then the present numbers will be of the form a2 + b2 -2ab which is equal to (a-b)2 next write down the numbers present in the above form i.e 22 + (9/2)2 - 2*2*(9/2) = 72 + (9/2)2 -2*7*(9/2)
  
• Then write them in their consized form like (2-(9/2))2 = (7-(9/2))2
  
• Take square root on both sides so we get (2-(9/2)) = (7-(9/2))
• Then move the calculated number from lhs to rhs so that the number gets cancled.Which produces the desired result i.e 2 = 7 -(9/2)+(9/2) => 2 = 7 .Hence proved
  

Proof of -*- = +

Product of two negative numbers always gives a positive number...

How ?

Here how it is.... "-" always means the opposite direction..

Consider the following number line

----|-----|-----|-----|-----|-----|---...
-3 -2 - 1 0 1 2 3 4 5 6

Now we know that what multiplication means...

2X3 means 2 added 3 times 2+2+2=6

Incase of a negative number
-1X2 means -1 added 2 times -1-1=-2

Incase of both the negatives...
-1X-3 is going in the opposite direction on the number line

----|-----|-----|-----|-----|-----|---... (-3 times from 0)
-3 -2 - 1 0 1 2 3 4 5 6
|____________|

So, 0-(-3)=3

graphical explanation

Direction

It is all about direction. Remember the Number Line?

Well here we have Baby krishna taking his first steps. He takes 2 paces at a time, and does this three times, so he moves 3 x 2 = 6 steps forward:

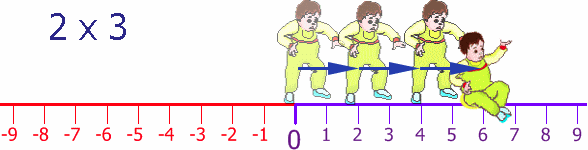
Now, Baby krishna can also step backwards (he is a clever little guy). His Dad puts him back at the start and then krishna steps backwards 2 steps, and does this three times:

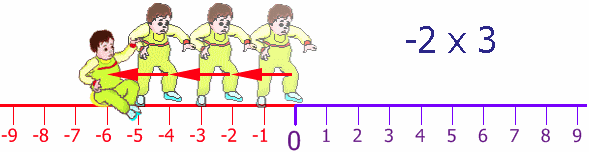
Once again krishna's Dad puts him back at the start, but facing the other way.krishna takes 2 steps forward (for him!) but he is heading in the negative direction. He does this 3 times:

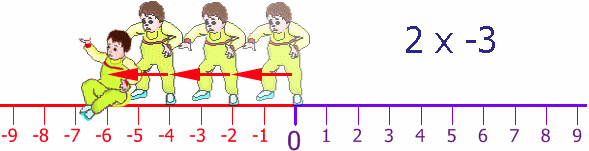
Back at the start again (thanks Dad!), still facing in the negative direction, he tries his backwards walking, once again taking two steps at a time, and he does this three times:

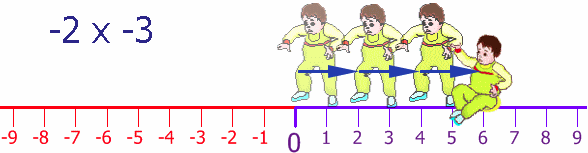
So, by walking backwards, while facing in the negative direction, he moves in the positive direction.

And That's All !

and finally

Axiom based proofs

1) a*0 = a*0 + 0 = a*(b + -b) + ab + -(ab) = a(b + -b + b) + -(ab) = ab + -(ab) = 0

2) 0*a = 0*a + 0 = (b + -b)*a + ba + -(ba) = (b+ -b + b)a + -(ba) = ba + -(ba) = 0

3) a*-a = a*-a + 0 = a*-a + (a*a + -(aa)) = a(-a + a) + -(aa) = a*0 + -(aa) = -(aa)

4) -a*-a = -a*-a + 0 = -a*-a + (a*-a + aa) = (-a + a)*-a + aa = 0*-a + aa = aa